SUMA DE VECTORES

La definición suma de vectores en el orden u+v produce otro vector, es como encadenar, siempre visualmente, un vector u y luego uno v. Diremos que u+v se simplifica como un vector w o que w descompone como suma de vectores u y v.

1) Decir que u+v=v+u, es exigir que las dos sumas simplifiquen en el mismo vector, en negro. Véase que en física los vectores en rojo simulan la descomposición de fuerzas ejercidas por el vector negro en su origen, y se representa con un paralelogramo.

2) Decir que u+(v+w)=(u+v)+w, es exigir que las simplificaciones de sumas de vectores puedan ser optativas en cualquier cadena de sumas.

3) Decir que existe un vector cero (elemento neutro) tal que u+0=u, equivale a exigir que exista un vector incapaz de efectuar, mediante la suma, modificación alguna a todos los vectores.

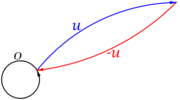
4) Decir que u+(-u)=0, es exigir la existencia de un elemento opuesto, -u, que sumado a u simplifique en un vector cero.

Tomado de: http://es.wikipedia.org/wiki/Vector